פונקציה חד-חד-ערכית ועל
(הופנה מהדף פונקציה חח"ע ועל)

בערך זה |
במתמטיקה, פונקציה חד-חד-ערכית ועל (נקראת גם בִּייקציָה; באנגלית: Bijection) מקבוצה X לקבוצה Y היא פונקציה המתאימה לכל איבר של X איבר אחד ויחיד של Y, כך שכל איבר ב Y מותאם לאיבר ב X. פונקציה חח"ע (חד חד ערכית) ועל נקראת "פונקציה הפיכה" וגם זיווג.
באופן פורמלי: חד-חד-ערכית ועל אם ורק אם לכל קיים יחיד כך ש . בתנאי זה, קיומו של מבטא את העובדה שהפונקציה היא פונקציה על, והיחידות שלו (כלומר העובדה שלא קיימים שונים שעבורם ), מבטאת את העובדה שהפונקציה חד-חד-ערכית.
דוגמאות
- מכירת כרטיסי קולנוע יוצרת התאמה בין קהל הצופים לבין הכיסאות שבאולם הקולנוע. כאשר כל הכרטיסים נמכרו, זו התאמה חד-חד-ערכית ועל - לכל כיסא באולם הקולנוע מותאם צופה אחד ויחיד. כאשר לא כל הכרטיסים נמכרו, זו התאמה חד-חד-ערכית שאינה על - יש כיסאות פנויים באולם.
- פונקציה המתאימה לכל מספר זוגי את החצי שלו (כלומר מתאימה ל-2 את 1, ל-4 את 2, ל-6 את 3 וכו') היא פונקציה חד-חד-ערכית ועל מקבוצת המספרים הזוגיים לקבוצת המספרים הטבעיים.

- הפונקציה היא חד-חד-ערכית ועל בתחום , משום שכל ערך של y בקטע הממשי מתקבל בדיוק פעם אחת. הפונקציה איננה חד-חד-ערכית בתחום משום שכל ערך של y בקטע הממשי מתקבל פעמיים (הערך 4, למשל, הוא וגם ).
- הפונקציה היא חד-חד-ערכית ועל בתחום , משום שכל ערך של y בקטע הממשי מתקבל בדיוק פעם אחת.
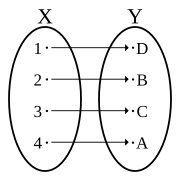
דיאגרמות להמחשה
-
פונקציה חד-חד-ערכית ועל
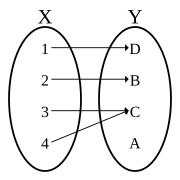
-
פונקציה חד-חד-ערכית שאינה על
-
פונקציה על שאינה חד-חד-ערכית
-
פונקציה שאינה חד-חד-ערכית ואינה על
-
מיפוי שאינו פונקציה כי חסר יעד ייחודי לאחד המקורות
תכונות ושימושים
- אם קיימת פונקציה כזו בין ל-, הקבוצות ו- נקראות "שקולות" והן בעלות אותה העוצמה.
- פונקציה היא חד-חד-ערכית ועל אם ורק אם היא הפיכה, ולכן היא מגדירה יחס שקילות בין קבוצות על פי עוצמתן ובפרט יחס סימטרי.
- אם על הקבוצות מוגדר מבנה נוסף (פעולות אלגבריות, טופולוגיה, מטריקה וכדומה), אז פונקציה חד-חד-ערכית ועל ביניהן השומרת על המבנה נקראת איזומורפיזם.
- פונקציה חד-חד-ערכית ועל מקבוצה אל עצמה נקראת תמורה.
- אוסף התמורות על קבוצה הוא חבורת הסימטריות של הקבוצה; לדוגמה, הפונקציה המתאימה לכל מספר שלם את העוקב שלו, היא תמורה על המספרים השלמים.
- פונקציות חד-חד-ערכיות ועל הן מאבני הבניין של צפנים סימטריים מודרניים רבים בקריפטוגרפיה.
ראו גם
קישורים חיצוניים
- פונקציה חד-חד-ערכית ועל, באתר אנציקלופדיה למתמטיקה (באנגלית)
- String Module Error: Target string is empty.html פונקציה חד-חד-ערכית ועל, באתר MathWorld (באנגלית) המזהה לא מולא ולא נמצא בוויקינתונים, נא למלא את הפרמטר.
| נושאים בתורת הקבוצות | ||
|---|---|---|
| מושגי יסוד | תורת הקבוצות הנאיבית • תורת הקבוצות האקסיומטית • קבוצה • יחידון • הקבוצה הריקה • קבוצת החזקה | |
| פעולות | איחוד • חיתוך • משלים • הפרש סימטרי • מכפלה קרטזית | |
| יחסים | יחס • יחס רפלקסיבי • יחס סימטרי • יחס אנטי-סימטרי • יחס טרנזיטיבי • יחס שקילות • יחס הופכי | |
| פונקציות | פונקציה • פונקציה חד-חד-ערכית • פונקציה על • פונקציה חד-חד-ערכית ועל • פונקציית הזיווג של קנטור | |
| משפטים | האלכסון של קנטור • משפט קנטור-שרדר-ברנשטיין • הלמה של צורן • משפט הסדר הטוב | |
| סדר | סדר חלקי • סדר מלא • סדר טוב • טיפוס סדר • מספר סודר | |
| עוצמות | עוצמה • קבוצה בת מנייה • קבוצה שאינה בת מנייה • עוצמת הרצף | |
| אקסיומות | אקסיומת ההיקפיות • אקסיומת האיחוד • אקסיומת הקבוצה האינסופית • אקסיומת ההחלפה • אקסיומת קבוצת החזקה • אקסיומת היסוד • אקסיומת הבחירה | |
| שונות | הפרדוקס של ראסל • השערת הרצף | |